Determinization example – nondeterministic FSM to deterministic

Here we describe one more example – the transformation of a nondeterministic automaton (FSM) to a deterministic one. Automata are assumed to be language recognizers (no output), a nondeterministic one can have many initial states and many final states, a string belongs to the language if there is a path from an initial to a final state marked by this string (empty or lambda moves are not included). Thus a simplest possible definition is assumed. For deterministic automaton the standard language recognizer definition is used. Automata are defined as sets consisting of state, event (=input alphabet element) and transition instances. The classical determinization algorithm is implemented – explore the state powerset (set of all subsets) space, by starting from the "initial set" and trying to expand the reachable set of statesets by applying transitions for all possible events and analyzing whether a new stateset has been reached by the given event (or it is a copy of existing one). When nothing more can be reached, the reached powerset elements are coded as new states of the deterministic FSM, and new transitions are defined accordingly, as well as the initial state and final states.

Actually, the example is a slightly extended version of a part of MOLA team paper for MTIP 05 workshop.

Fig. 1 shows the metamodel (source = target), with the StateSet class used during the algorithm run. Fig. 2 – 6 show the main MOLA program and subprograms implementing the abovementioned algorithm. Some of the subprograms use additional MOLA elements not used in the main example.

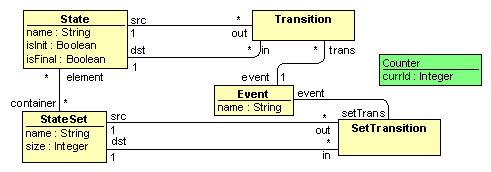
Fig. 1. Metamodel of automatons.

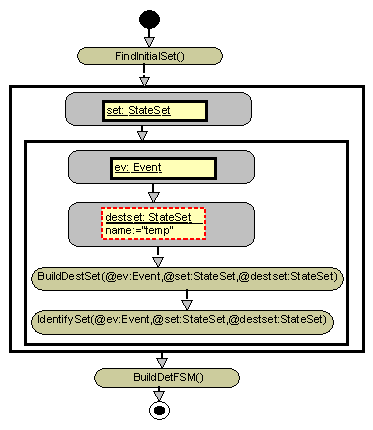
Fig. 2. Main MOLA program for the determinization.

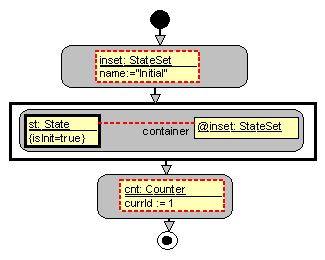
Fig. 3. Subprogram FindInitialSet.

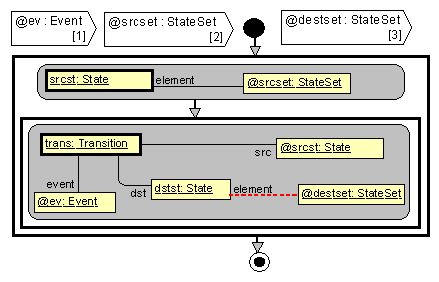
Fig. 4. Subprogram BuildDestSet.

The next subprogram IdentifySet uses more complicated OCL expressions in constraints – subexpressions of the form element_name.role_name, which denote an instance set (if the multiplicity is *) and elementary OCL operations on sets (here – the set equality). Two special control constructs – explicit continue (flow to the loop border) and return (flow to end symbol) are used in the first loop.

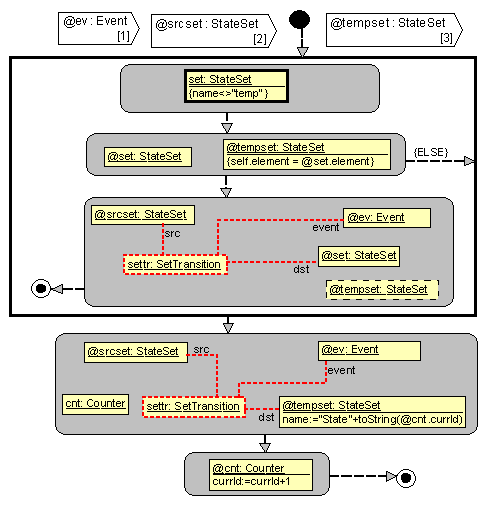
Fig. 5. Subprogram IdentifySet.

The subprogram BuildDetFSM also uses OCL set operations in constraints – notEmpty (while the existence of a Final State is specified by a pattern element).

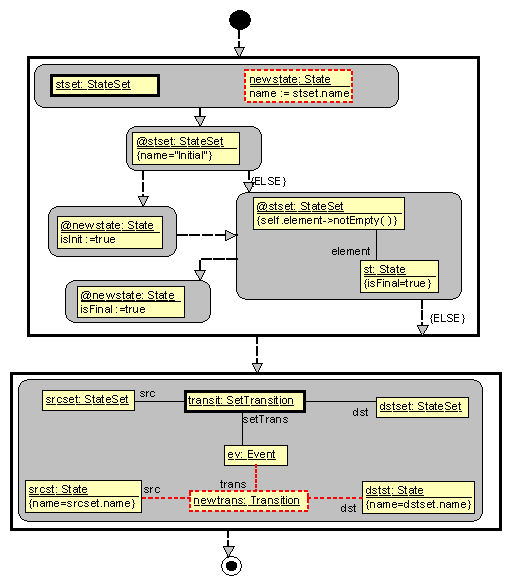
Fig. 6. Subprogram BuildDetFSM.

Authors consider this example also a right balance between the textual and graphical style of transformation specifications. Namely to make the example maximally readable, explicit sets defined via associations from an instance and OCL set operations are used in patterns. Certainly, the example could be specified "100% graphically", using nested loops, but this seems not to be the best choice. The used OCL elements are already implemented in MOLA tool.

In order to make a diagram-based test driver for the example, the metamodel has to be extended slightly. Classes for the diagram itself are added, as well as parts of target model are made separate from source model. Fig. 7 shows the extended metamodel.

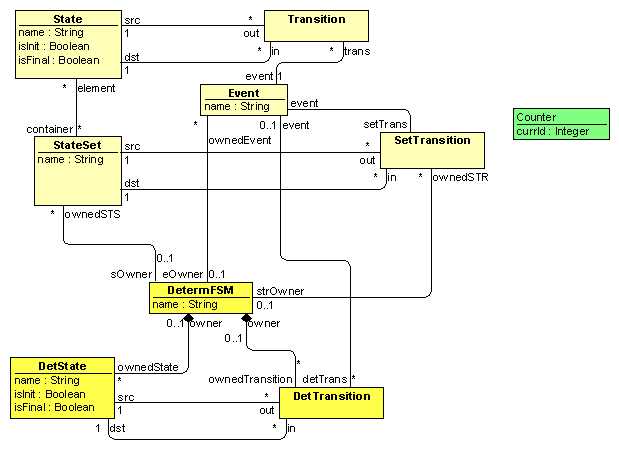
Fig. 7. Extended Metamodel of automatons

Accordingly, the BuildDetFSM subprogram is extended by some scaffolding actions for building the target diagram (actually, its domain counterpart) – see Fig. 8. All temporary elements are also linked to this diagram – in order to make the evaluation of test results easier.

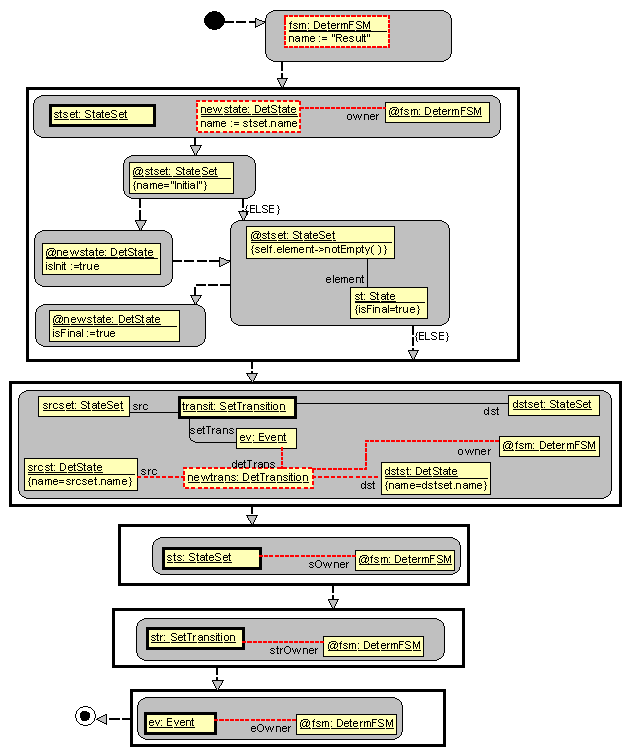
Fig. 8. Extended subprogram BuildDetFSM.

A nodeterministic test automaton (diagram) is shown in fig.9, but its determinization result in Fig. 10.

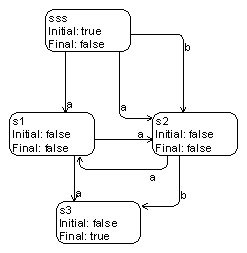
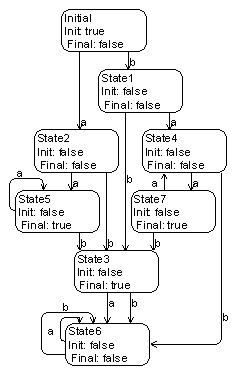
Fig. 9 Nondeterministic automaton example Fig. 10 Result of determinization

To make the tracing between these two automatons easier, part of the "debug tree" is also shown:

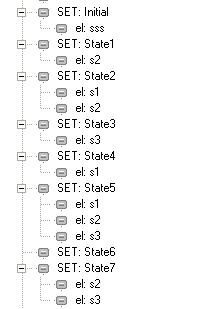
Thus it is comparatively easy to ascertain that the transformation is correct (at least, on this example).